2021. 6. 12. 16:38ㆍMath
[목차]
1. 선형분류의 목표와 방법들
2. 판별함수
3. 분류를 위한 최소제곱법
4. 퍼셉트론 알고리즘(The Perceptron algorithm)
5. 확률적 생성 모델 (Probabilistic generative models)
6. 확률별 식별 모델 (probabilistic discriminative models)
===============================================
1. 선형분류의 목표와 방법들

2. 판별함수 Discriminant Functions
- 확률을 직접 계산하진 않고, 바로 클래스 할당
- ex) binary class
결정경계 : y=0으로 두었을 때의 2개의 벡터로 만들어짐
그림의 이해


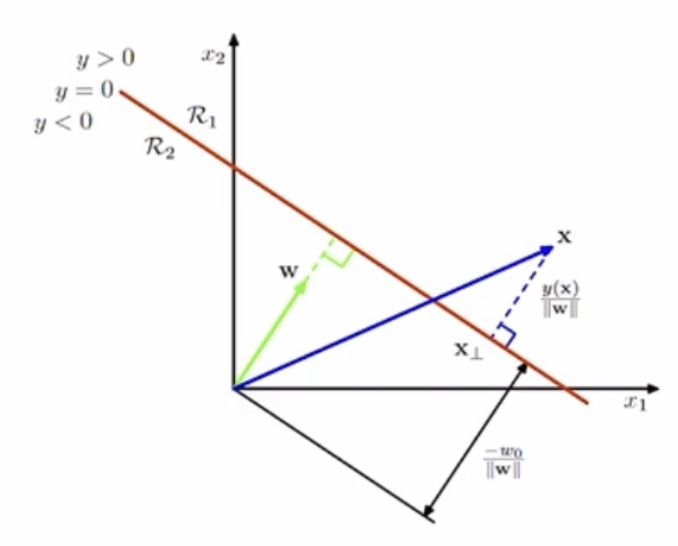
빨간선 = y=0일 때, decision boundary : 즉 빨간색보다 위에 있으면(y>0) 클래스 1 , 빨간색보다 아래 있으면(y<0) 클래스 2
원점에서 경계면까지의 거리 (r) = 벡터 W projection
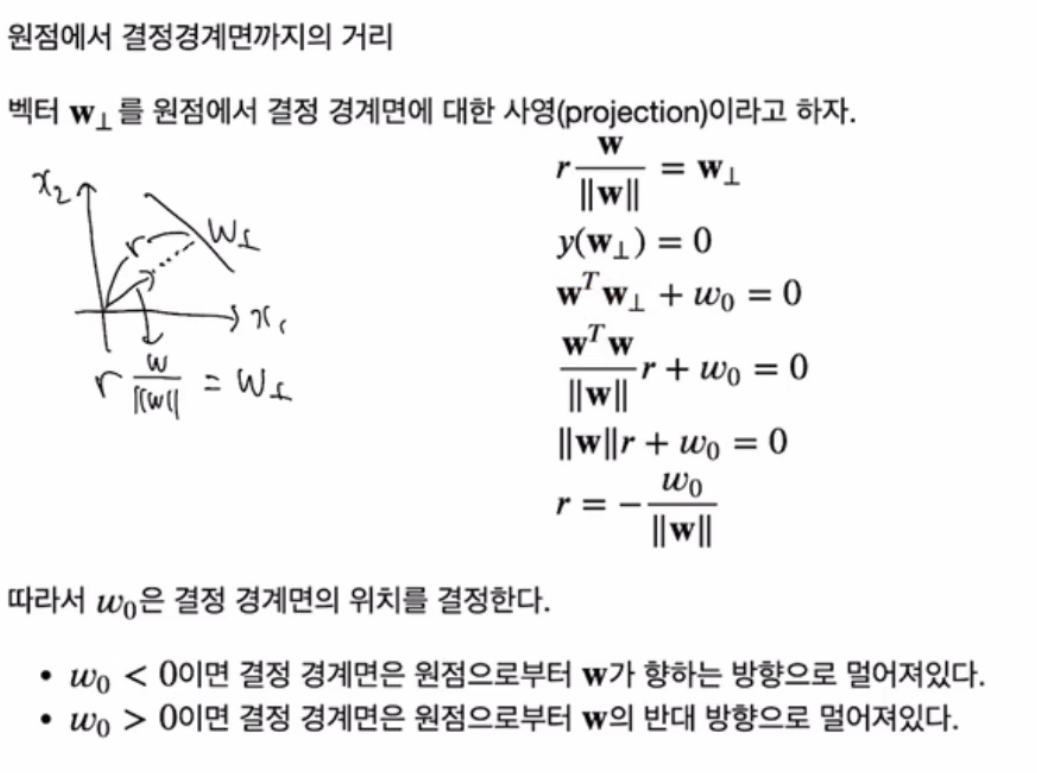

풀어쓰면
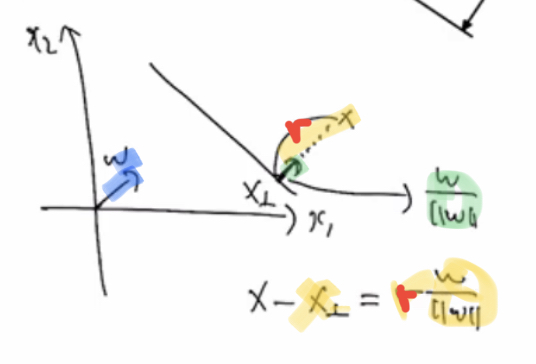
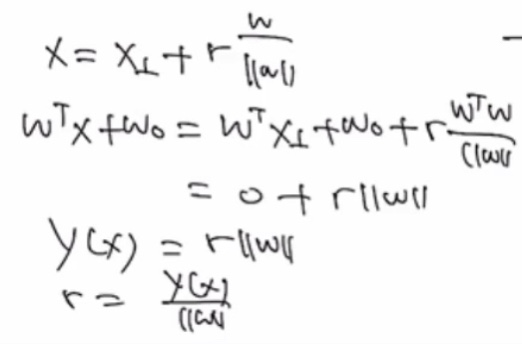

3. 분류를 위한 최소제곱법(Least Squares for classification)
실수 공간에서의 회귀 문제 대비.. 분류 문제에서의 최소제곱법은 그렇게 좋은 방법은 아니다
binary classification (첫번째 클래스 = 1, 두번째 클래스 = 0)



제곱합 에러 함수
- 여기에서의 W는 행렬이다 !! 하나의 값이 아님
- 그래서 trace로 표현해서 행렬 미분을 통해 에러함수를 최소화하는 W를 찾을 수 있다
- 방금 구한 w를 대입하면 판별함수 y(x)를 찾을 수 있다
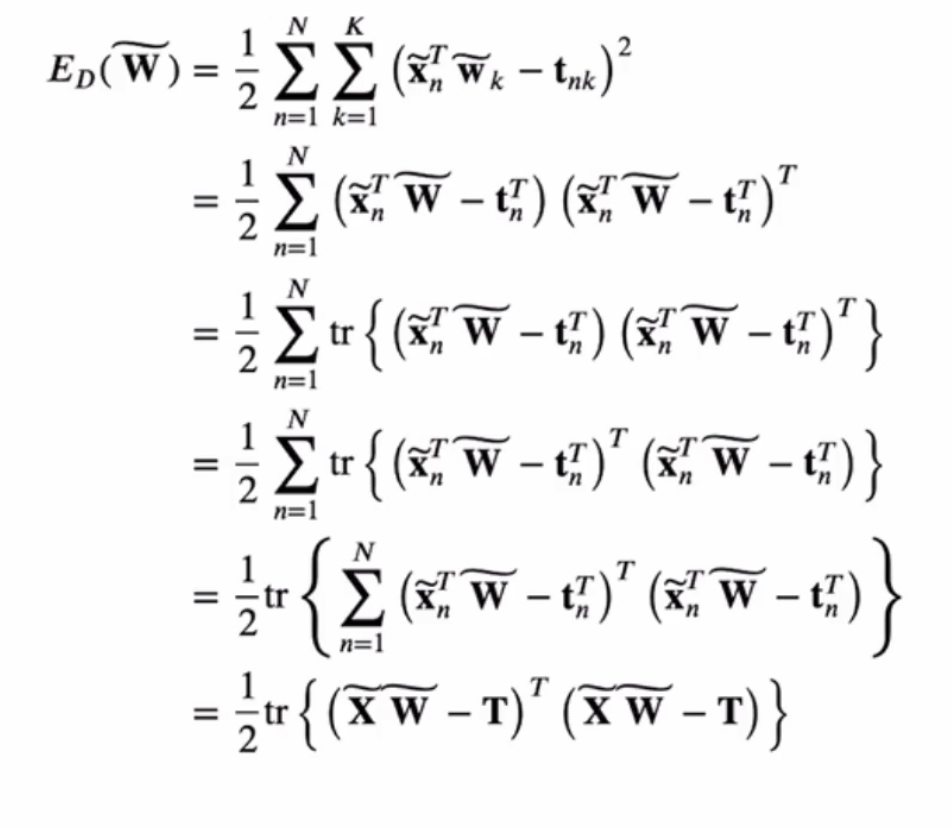

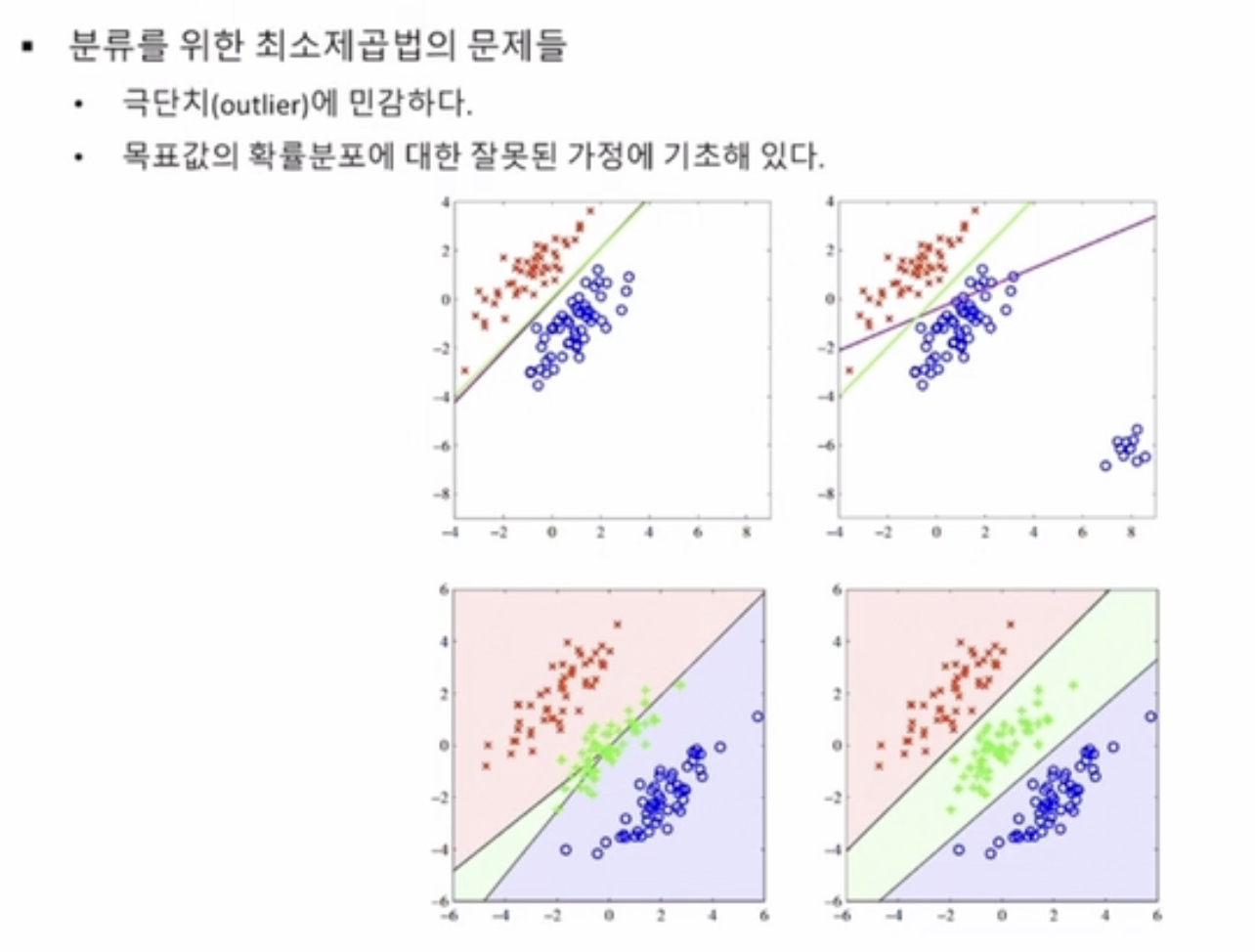
단점
그림에서 보라색 = 최소제곱법으로 찾은 판별함수 vs 녹색 = 로지스틱 회귀
1. 극단치에 민감
2. 목표값의 확률분포 다르게 정의 - 잘못된 에러함수는 잘못된 결과를 유도해버린다
4. 퍼셉트론 알고리즘(The Perceptron algorithm)
목표값 t = -1 or 1 두 개를 가진다고 가정 (첫번째 클래스 = 1, 두번째 클래스 = -1)
에러함수 E(W) 를 사용하여 에러 최소화 추구

Stochastic GD 의 적용
tau = iteration 의 숫자
잘못 분류된 샘플에 대한 업데이트 실행 하다보면 점점 에러가 줄어감
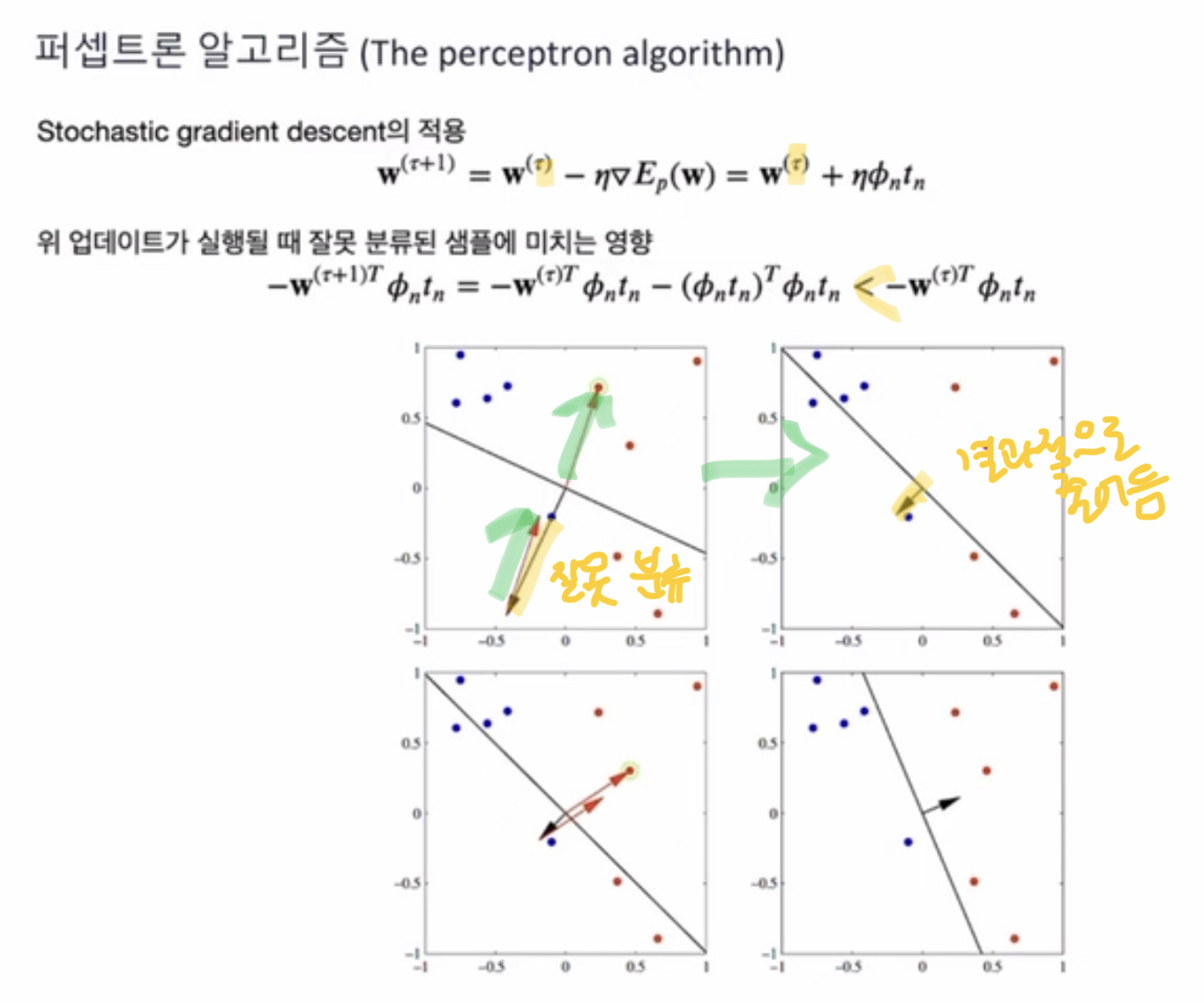
특징
1. 최소제곱법보단 퍼셉트론 알고리즘이 좋다
2. 60년대부터 시작된 오래된 모델이지만, 뉴럴 네트워크의 기초가 됨
5. 확률적 생성 모델 (Probabilistic generative models)
확률적 모델
1) 생성모델
2) 식별모델
클래스가 주어졌을 때의 x의 확률과, 클래스의 확률을 구해서 -> (베이즈 정리) -> 사후 확률

a에 대한 로지스틱 시그모이드 함수
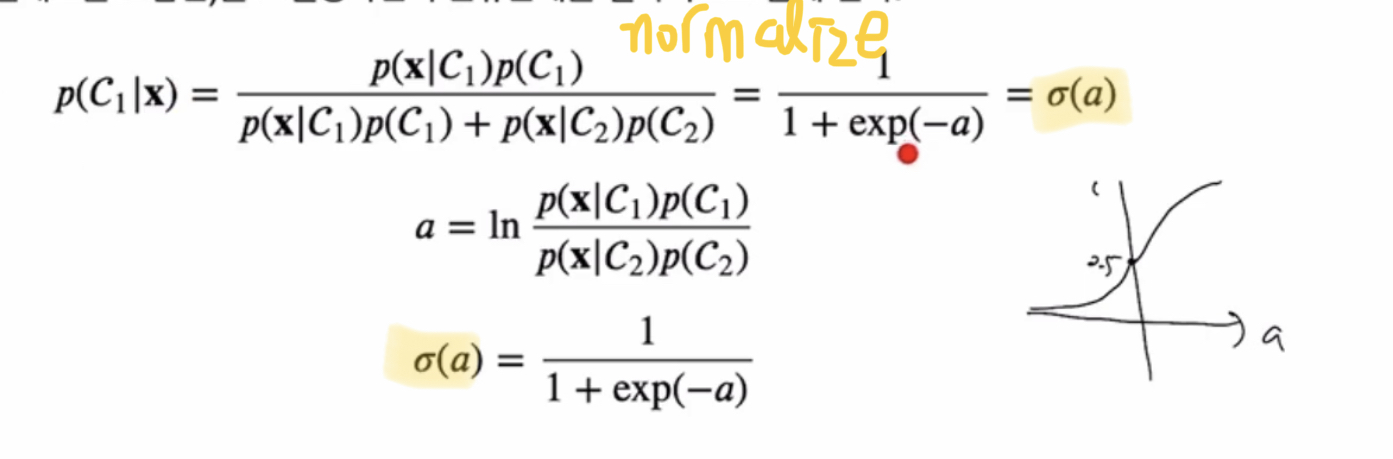
a가 특정한 선형 함수 형태를 가지게 될 떄 이 모델은 “generalized linear model” 이라고 부른다
Logistic Sigmoid 함수
클래스가 3개 이상이면,
ak 식 중요

연속적 입력 (Continuous inputs)
가정1) class density (p( x | class K) ) 가 가우시안 분포를 따르다
가정2) p( x | class K)가 모든 클래스에 대해 공분산이 동일하다

확률은 x에 대한 선형식으로 표현된다
확률이 가지는 결정경계는 x에 대한 선형식으로 찾을 수 있다
w벡터와 wo는 (식이 나와있지만) 실은 모두 파라미터로, 모델에서 데이터 넣어서 학습해야할 부분
왜 선형식으로 나타날까? p( x | class K)가 모든 클래스에 대해 공분산이 동일하다고 가정했으니까
클래스별로 공분산이 다르면, 조건부확률도 비선형이 된다
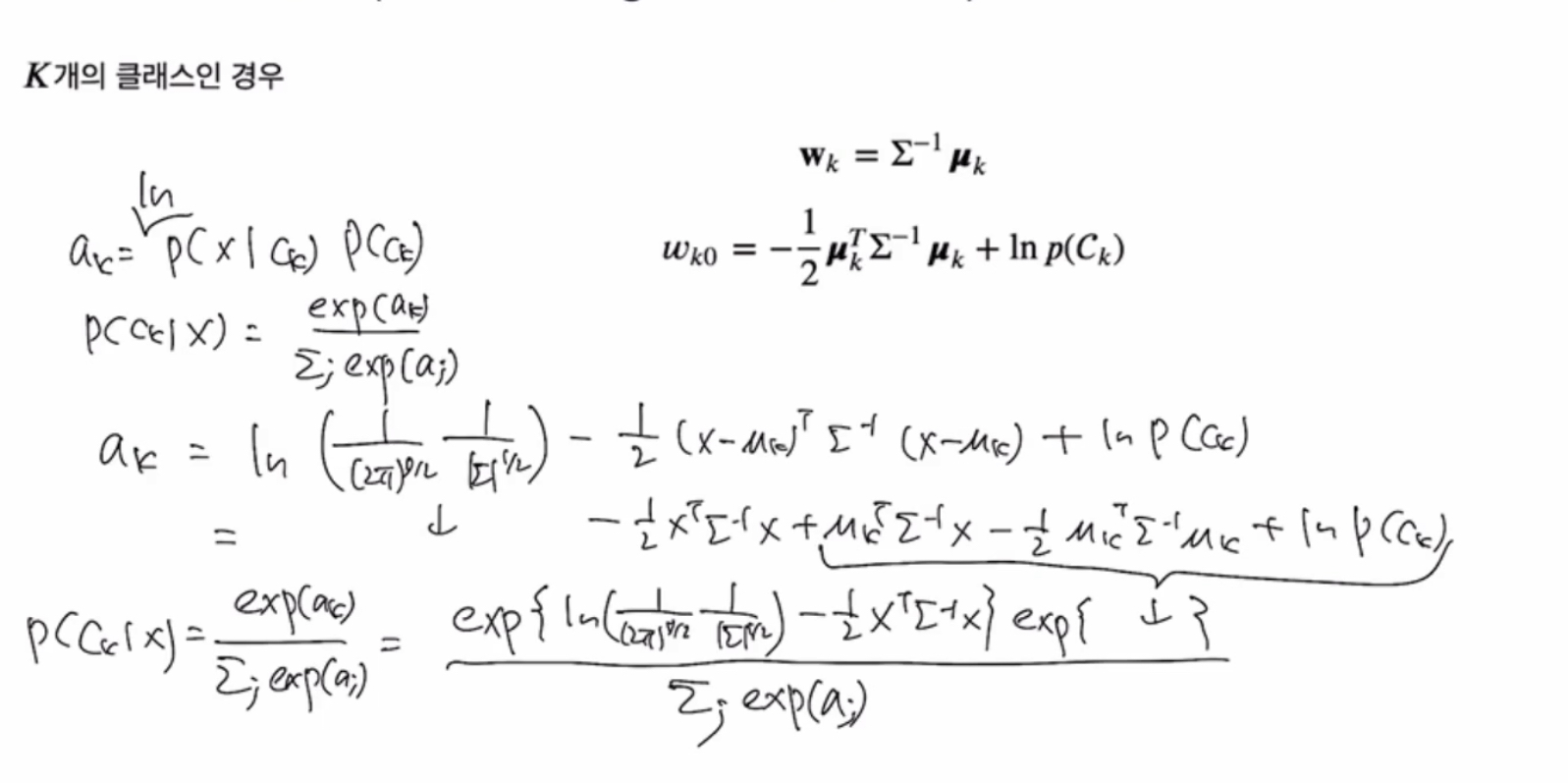
우도식을 최대화하는 파라미터 찾기
최대우도해(Maximum Likelihood Solution)

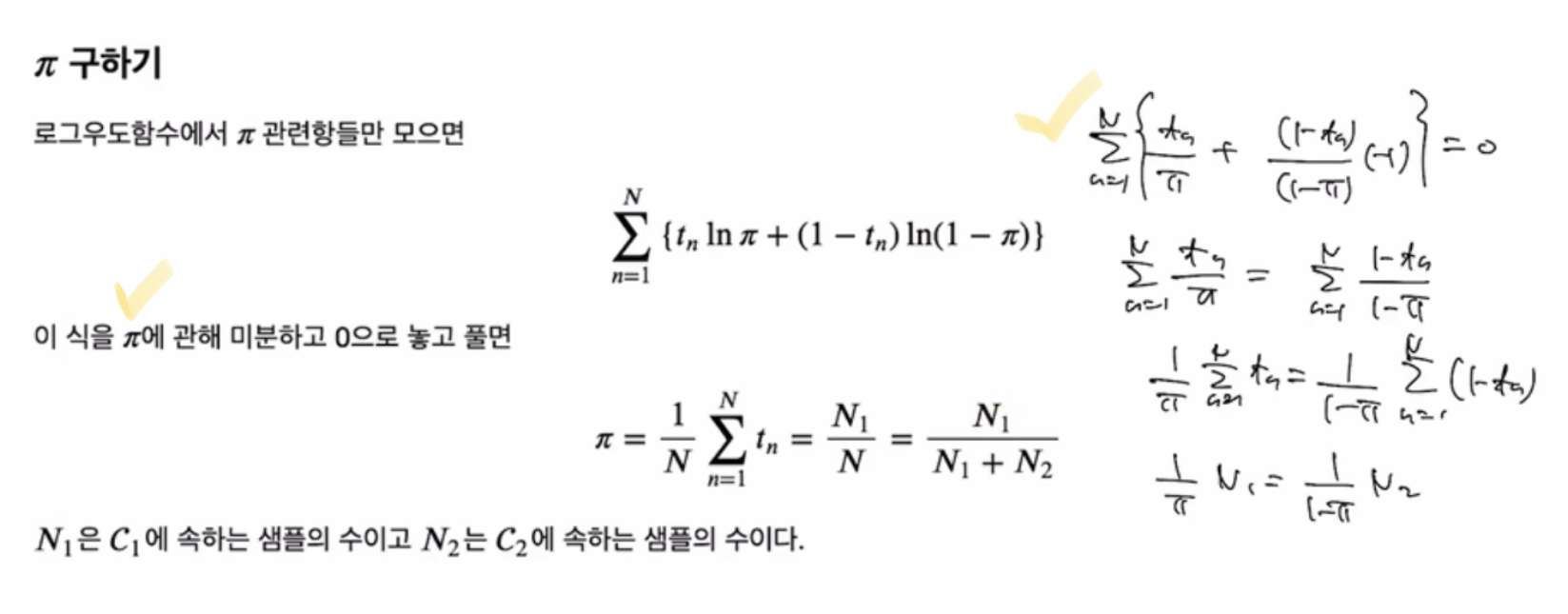
phi 구하기
mu1, mu2 구하기

공분산 행렬 구하기



입력이 이산형일 경우
- 모든 특성들이 확률적으로 독립이라는 가정 하에 (= 나이브 베이즈 가정 하에) 하면
클래스 k일 때의 x의 확률이 단순하게/쉽게 분해되고,
결정경계도 ‘선형’으로 도출됨
입력이 연속형일 경우

6. 확률별 식별 모델 (probabilistic discriminative models)
확률적 생성모델 - x의 선형함수를 softmax나 logistic sigmoid를 통과해서 표현 되었다. 그러나 구해야할 파라미터가 참 많았쥐. 특히 공분산행렬 파라미터 많이 구해야하는데, 심지어 quadrantic 문제였다.
확률적 식별 모델 - 사후확률을 가정하고, 바로 구하기
x대신에 파이 기저함수 사용

최대우도해


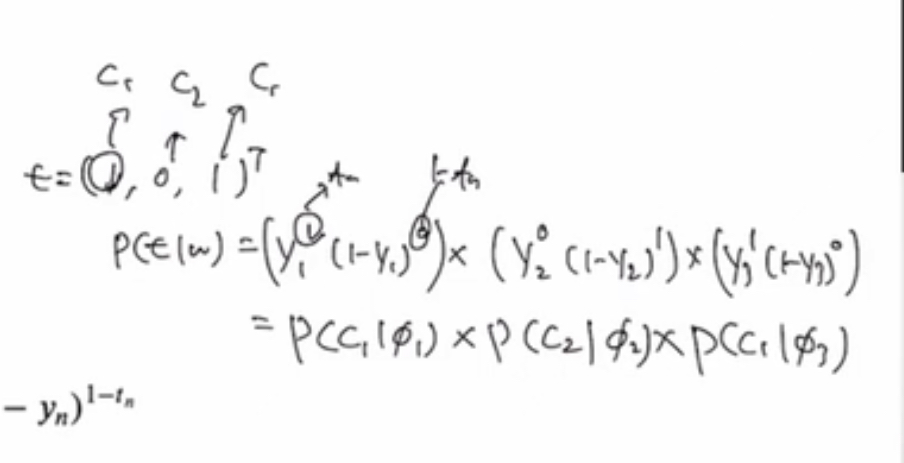
조건부확률 = x1일 때 class= 1 일 확률 * x2일 때 class= 0 일 확률 * x3일 때 class= 1 일 확률

크로스엔트로피
- 정보이론
- p와 q 두 개의 확률분포가 주어졌을 때, x의 확률분포에 대한 기대값 계산
- 크로스 엔트로피 최소화 = 두 확률분포 차이의 최소화 = 우도의 최대화 = 모델 예측값(분포)과 목표변수(분포) 차이 최소화
'Math' 카테고리의 다른 글
| 3차원 그래프 그리기 (0) | 2024.06.13 |
|---|---|
| 메타 인터뷰 질문 (0) | 2022.05.20 |
| Machine Learning 기초 (1) - 선형 회귀 Linear Models for Regression (0) | 2021.06.12 |
| 확률분포 (3) - 연속확률분포 가우시안분포 (1) | 2021.06.11 |
| 확률분포 (2) - 이산확률분포 다항변수 (0) | 2021.06.07 |