2021. 6. 12. 13:08ㆍMath
[목차]
1. 선형 기저 함수 모형
2. 최대우도와 최소제곱법 -> 편향 파라미터 w0 와 b의 최적의 우도 구하기
3. Maximum Likelihood의 기하학적 의미
4. 온라인 학습(Sequential Learning) - Large linear regression
5. 규제화된 최소제곱법 (Regularized Least Squares)
6. 편향 분산 분해(Bias-Variance Decomposition)
7. 베이지안 선형회귀 (Bayesian Linear Regression)
=======================================
1. 선형 기저 함수 모델

x는 비선형이라도 w는 선형!!!!

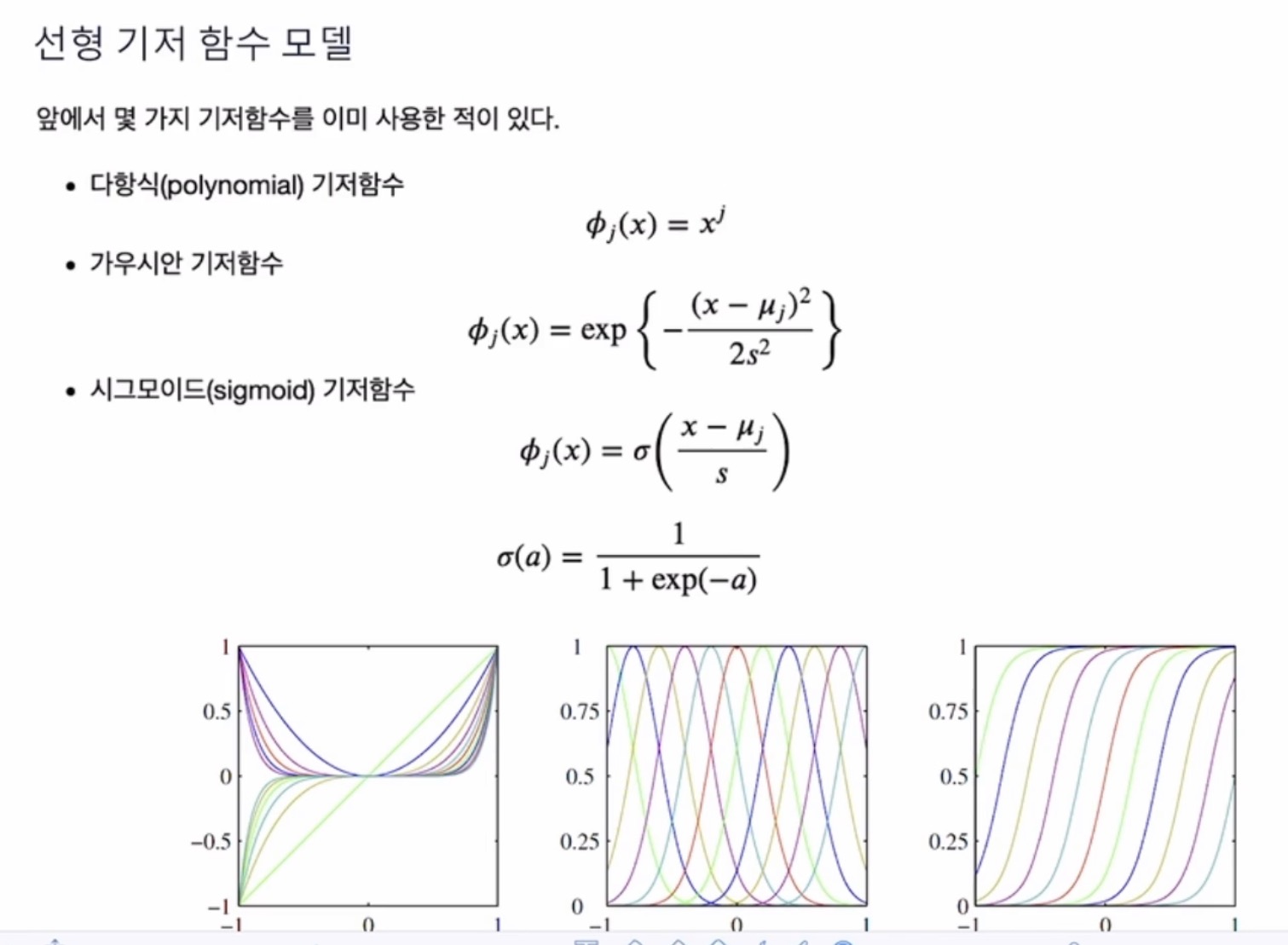
선형 기저 함수의 예시
ex) 다항식 기저함수 = j에 따라서 얼마나 x를 제곱해줄 것인지
가우시안 기저함수 - s에 따라서 얼마나 옆으로 퍼지는지, mu에 따른 위치
시그모이드 기저함수 - 모든 값을 0~1 사이로 변환
기저함수 안에 들어가는 x는 모든 x
2. 최대우도와 최소제곱법(Maximum Likelihood and Least Squares)
결정이론을 상기해보면, t가 t = y(x,w) + c 라는 분포를 따를 때, 조건부 기대값은 y(x, w) 값이 된다.
즉, 우리의 최선은 ”최적의 w”를 알고 있어서, 새로운 x값이 들어올 때 y의 값을 구하여 예측하는 것

최적의 w는 어떻게 찾을 것인가?
우도를 표현한다 = 출력값 t의 확률값을 계산한다

입력값 X는 벡터
입력값 X는 조건부 에 포함됨, 단 X가 명확한 경우, 조건부 파트에서 생략되기도 함
n개의 가우시안 분포를 곱해서 로그를 취해주어서 로그 우도함수 계산
t를 가우시안 분포로 정의했을 때
최적의 w = 우도함수의 최대화 = 제곱 에러의 최소화
최적의 Wml (ml = maximum likelihood)


각각의 기저함수는 n개의 파라미터를 가진다
design matrix는 ( nxn 형태의) square-matrix가 아닐 수 있어서(때로는 input의 개수보다 feature의 개수가 더 많은 경우도 있어서)
w를 바로 design matrix의 역행렬을 써서 구하는게 아니라
normal equation 형태로 계산해서 구한다

Normal Equation 유도할 때
design matrix와 weight 곱하면 예측값 t 의 분포를 따른다
이 에러의 제곱을 최소화하는 문제로 푼다고 하면
1/2 곱하는 이유 - 어차피 최소값 구하니까 반으로 쪼개도 다를 바 없다 ??
에러함수 E(w)를 w에 대해서 미분하고
미분값 = 0 으로 놓고 w에 대해서 풀면
“파이의 transpose 와 파이”를 곱하게 되면(파란색 부분) square -matrix 이므로 역행렬을 구할 수 있다
역행렬이 존재하게 되면(“파이의 transpose 와 파이”(파란색 부분)의 역행렬)
w를 구할 수 있다
design matrix(파이)의 모든 열들이 서로 선형독립이라면 “파이의 transpose 와 파이”(파란색 부분)는 역행렬이 존재한다
항상 성립하는 것은 아니다, 대부분은 성립함
w0에 대한 최대우도해 구하기
w0 = 예측값t의 평균 - 하나의 기저함수를 m개의 데이터에 대해서 평균 낸 것
합과 목표값의 사이를 보정해주는 역할
precision 베타의 최적값
우도를 미분한 값, 목표값 으로부터 분산되어 있는 정도
3. Maximum Likelihood의 기하학적 의미

span (생성) = a값들의 곱의 합으로 나타낼 수 있는 벡터 v의 모든 가능한 집합

range(치역) = 모든 열들에 대한 생성. 임의의 A를 곱해서 나타낼 수 있는 모든 v의 집합
projection(사영) = 벡터를 span에 속해있는 벡터 중에서 t와 가장 가까운 벡터
만약 span이 주어진 게 아니라, 행렬 A가 주어져있으면, 행렬 A의 치역으로 projection 됨
A 대신 디자인 매트릭스 (파이) 쓰게 되면, 이는 W maximum likelihood에 파이를 곱한 값
타겟 벡터 t가 있고, 파이? 라는 벡터들이 있을 때
파이란 각 열벡터의 집합 = 치역을 나타내는 집합
(참고) 공간 매트릭스는 디자인 매트릭스 (파이)의 치역을 나타내는 지역
해당 치역을 나타내는 집합에서 목표값 t와 가장 가까운 벡터는?
-> 가장 가까운 지점을 찾기 위해서는, 수직으로 내려서 y를 구한다
4. 온라인 학습(Sequential Learning)
온라인 학습
= 대규모 데이터 다룰 때, 일부의 데이터만 활용하여 학습
(+) 데이터가 많아도 온라인 학습 방식으로 학습 가능, 시간이 걸려도 메모리 적게 쓰면서 계산하기 때문에 메모리 부담은 줄일 수 있다

대표적인 예시가 Stochastic Gradient Descent
기저함수 Xn이 주어졌을 때,
Gradient Descent는 전체 n값에 대해서 기울기를 구하게 되지만 vs. SGD는 하나의 n에 대해서(Xn) 기울기 구해서 업데이트
n_iter를 통해서 x데이터 전체를 다 읽고나서도, 여러번 반복적으로 다시 읽으면서, w를 업데이트할 수 있다
[실습] 대규모의 선형회귀 (주피터 노트북 참조)
우리는 normal equation을 사용하고 싶은데, 데이터가 너무 크면(메모리에 다 안 들어갈 정도이면) 어떻게 학습을 시킬까?
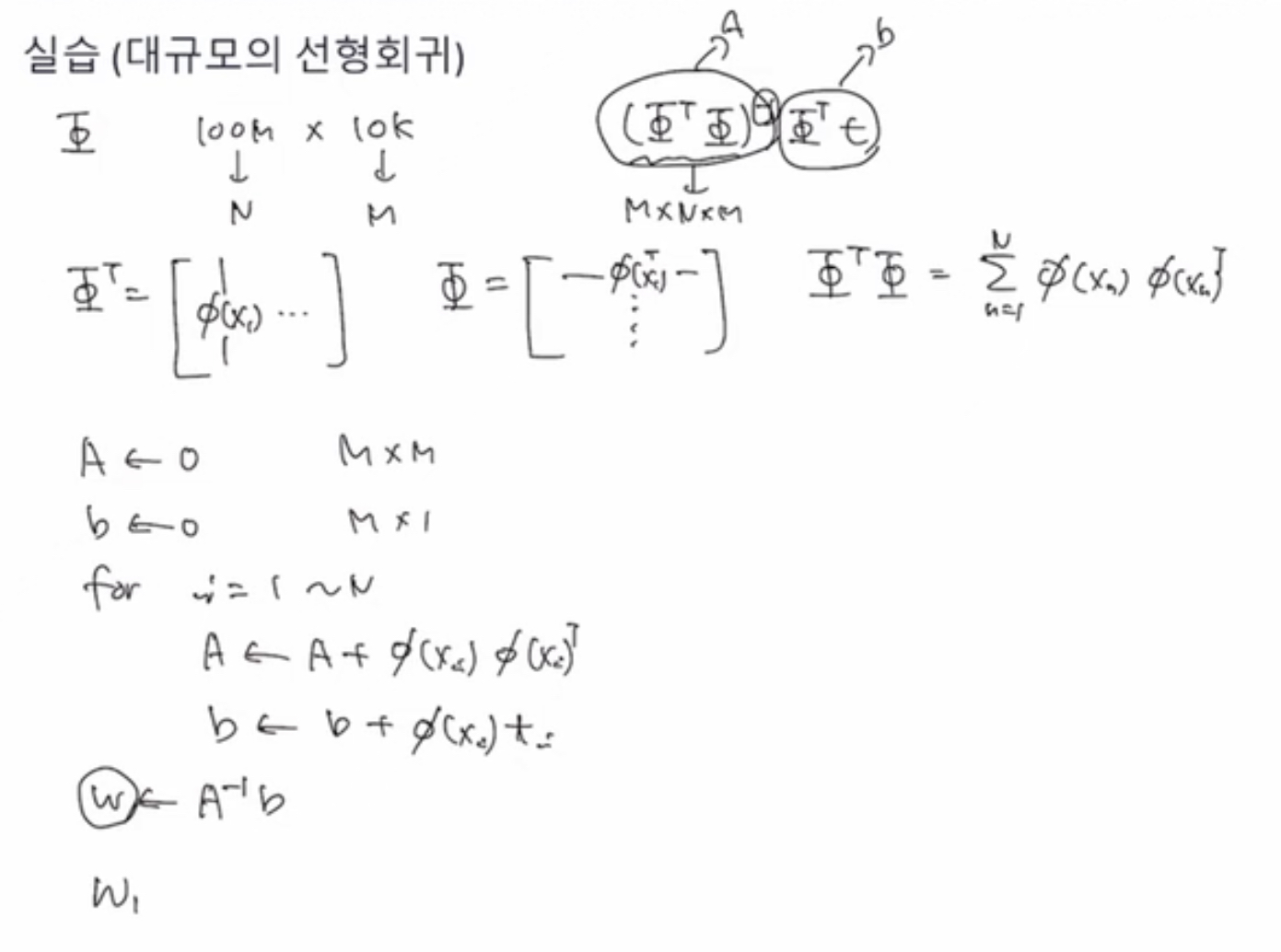
파이의 전치행렬과 파이를 곱하면, 열벡터 형태와 행벡터 형태를 곱하면 합의 형태로 나타나짐
합의 형태로 표현되는 결과는 행렬(outer product)임 (결국 n번만큼 더하게 되는 것)
= 즉, 데이터를 한번에 읽어내지 않더라도, 하나씩 하나씩 읽어들어서 내적값을 구해서 더해나가면 되는 것임
예를 들어, 모든 equation이 끝났을 때 A와 b를 구할 수 있음
그리고 Weight (maximum_likelihood) 찾을 수 있음
5. 규제화된 최소제곱법 (Regularized Least Squares)
규제화항 Ew(W) ~ lambda값에 따라 얼마나 규제화할지 조절할 수 있음

규제화항을 추가하여 w에 대해서 미분하고 풀게 되면
역시 , Maximum Likelihood를 풀 수 있음

그림에서 왼쪽이 L2 norm, 오른쪽이 L1 norm
만약 두 개의 element가 있을 때, 파란색 원 = 규제가 없을 때, 같은 error함수를 갖는 영역을 나타내는 등고선 같은 것
제약조건 만족(빨간색 영역 내에 있어야 한다) 시키는 최적의 w 찾기
1) 제약조건 q = 1 으로 두면, L1 norm
라그랑지 문제로 보면, inefficient constraints를 만족하는 최적화 문제로 볼 수 있다
제약조건을 만족시키려면 반드시 꼭지점 부분만 해당됨
꼭지점이라하면 다른 w는 0이 되는 것
->> sparse 한 결과가 된다 (0이 많아진다)
2) 제약조건 q = 2로 두면, L2 norm
6. 편향 분산 분해(Bias-Variance Decomposition)
모델의 과적합되는 현상

최적 예측값 = x가 주어졌을 때의 타겟y의 기대값
문제는 우리는 정확한 h(x)는 알 수 없고, 제한된 데이터셋 D만 알고 있다.
제한된 데이터로도 모델의 불확실성을 표현하는 방법은?
1) 베이지안
2) 빈도주의 : maximum likelihood = 여러 데이터의 평균을 구해보는 가상의 실험을 통해서, 점추정값의 불확실성을 해결
제한된 데이터셋 D에 대해 loss는 L(D)
여러 모델 을 비교할 때, 손실 값들의 평균을 구해서 손실값이 가장 낮은 모델을 선택하듯
여러 데이터셋을 비교하여, 해당 데이터셋의 기대값들의 평균을 생각해보자



Expected loss = 편향의 제곱 + variance + noise
편향의제곱 = 평균예측값 이 정확한 h(x)로부터 얼마나 떨어져있나
variance = 모델의 자유도가 높을수록(=모델의 복잡도가 높을수록 = 모델의 차수가 높을수록), 편향값이 나오는 경향이 있다.
>> 모델의 복잡도가 높을수록 각각의 예측값이 평균으로부터의 떨어진 경향이 크다, 각 예측값이 데이터셋에 sensitive하니까
우리는 Expected Loss 의 최소화를 목표로 하므로, bias와 variance의 trade-off 사이에서 적정한 값을 찾아야


왼쪽 빨간선 각각의 데이터셋, 오른쪽 빨간색 = 각 데이터셋의 평균
1. 자유도가 낮은 경우(심플한 모델) - 왼쪽 보니 분산은 작고, 오른쪽 보니 편차가 크다
3. 자유도가 복잡한 경우(주어진 데이터셋에 민감한 모델) - 왼쪽 보니 분산이 크고, 오른쪽 보니 편차는 낮다

이러한 빈도주의 방식으로는 매끄러운 결과가 나오지 않는다….
7. 베이지안 선형회귀 (Bayesian Linear Regression)
주어진 데이터가 작더라도, 모델의 불확실성(uncentain)을 잘 나타내기 위해서는 베이지안 선형회귀 방식을 통해 모든 확률값을 업데이트하는 방법을 쓴다

사전확률과 likelihood 알면 사후확률확률을 구할 수 있다
1)w의 사전확률은 m0라는 평균과 S0라는 공분산을 가진다
2) 우도
각각 가우시안 분포를 따르는 w에 대해서
각 t값은 모두 동일한 1/베타 만큼의 분포를 따르고, t값의 출력값은 = 파이로 써진 부분(선형모델)의 출력값의 평균
지수부를 풀어쓰면 위의 하단과 같이 기술됨


w의 사후확률도 가우시안 분포를 따르며,
mN일 때 최대사후확률인 w 를 갖는다
만약 alpha가 0에 가까워질수록 alpha 반대값은 무한히 커지게 되는데, 공분산 행렬 S는 0행렬에 가까워진다

사후확률에 로그를 씌워주면 규제항이 포함된 함수가 됨, L1, L2 규제항들은 특정한 형태인 셈
>> 빈도주의 방식보다 베이지안 선형 회귀가 훨씬 일반론적 방법이다
!!확률분포 이해의 중요성!!
'Math' 카테고리의 다른 글
| 메타 인터뷰 질문 (0) | 2022.05.20 |
|---|---|
| Machine Learning 기초 (2) - 선형 분류 Linear Models for Classification (0) | 2021.06.12 |
| 확률분포 (3) - 연속확률분포 가우시안분포 (1) | 2021.06.11 |
| 확률분포 (2) - 이산확률분포 다항변수 (0) | 2021.06.07 |
| 확률분포 (1) - 이산확률분포 이항변수 (0) | 2021.06.07 |