2021. 6. 11. 19:01ㆍMath
[목차]
1. 가우시안 분포의 기대값
2. 가우시안 분포의 공분산
3. 조건부 가우시안 분포
4. 주변 가우시안 분포(Marginal Gaussian Distributions)
5. 가우시안 분포를 위한 베이즈 정리(Bayes’ Theorem for Gaussian Variables)
=============================================
1. 가우시안 분포의 기대값

X는 벡터이고 X 의 기대값도 벡터이다
X1에 대한 기대값은 모든 x와 그 확률에 대해 적분한 값

가우시안 분포에서 x의 기대 값은
보기 쉽게 z로 변환하여 z에 대한 적분 으로 변형
아래의 식은 모든 Y 에 대한 적분
다시 한번 강조 하자면 결과 값은 벡터이다

이를 풀면 오른쪽 상단에 있는 하드 function으로 계산해 보면 값은 0이 됨
따라서 기대값은 mu가 됨
2. 가우시안 분포의 공분산

먼저 이차 적률을 구하는데 이는 X 의 제곱의 기대값을 의미한다
이를 치환하여
Z의 제곱으로 적분하면
X와 X 의 전치 행렬을 내적 한 것을 확률분포를 적분 한다
이렇게 계산하면 모든 i와 모든 j에 대한 내적 결과가 나오고
이 행렬은 주 대각선 외에는 모든 값이 0



조건부 가우시안 분포에서
x를 두 그룹으로 나눈다면
평균 벡터도 두 그룹, 공분산 행렬은 네 개의 그룹이 나온다
3. 조건부 가우시안 분포

다만 공분산 행렬의 역행렬 = 정확도 행렬
주의할 것은!!! 전체 행렬은 같으나,
행렬의 각 원소(예를 들어 lambda aa)가 같다는 것은 아니다

우리가 구하고자 하는 것은 Xb가 주어졌을 때 Xa의 조건부 확률
이 조건부 확률은 ‘완전제곱식’ 방법으로 구할 수 있다
(우리는 지금 단일변수에 대한 이차식을 계산하고 있다)

전체 x가 다 주어져있을 때의 결합밀도함수 p(Xa, Xb)에 대해서
이를 a에 대해서만 사용하는 함수 g(Xa)a로 변환하여 표현해보자
alpha = p(Xb) : 알파는 Xa에 대한 확률
알파는 Xb 에 대한 주변 확률 ? 결합밀도함수 ?
즉 Xa, Xb에 대해서 확률이 주어져있을 때의 확률분포 나타내는 g(x)를 찾는 문제
“평균벡터” “공분산행렬”이 중요.
조건부확률을 구할 때 꼭 타우는 알지 못해도 된다. 무시해도 된다.
지수부를 전개해보면

지수부를 파티션을 통해 정리하면
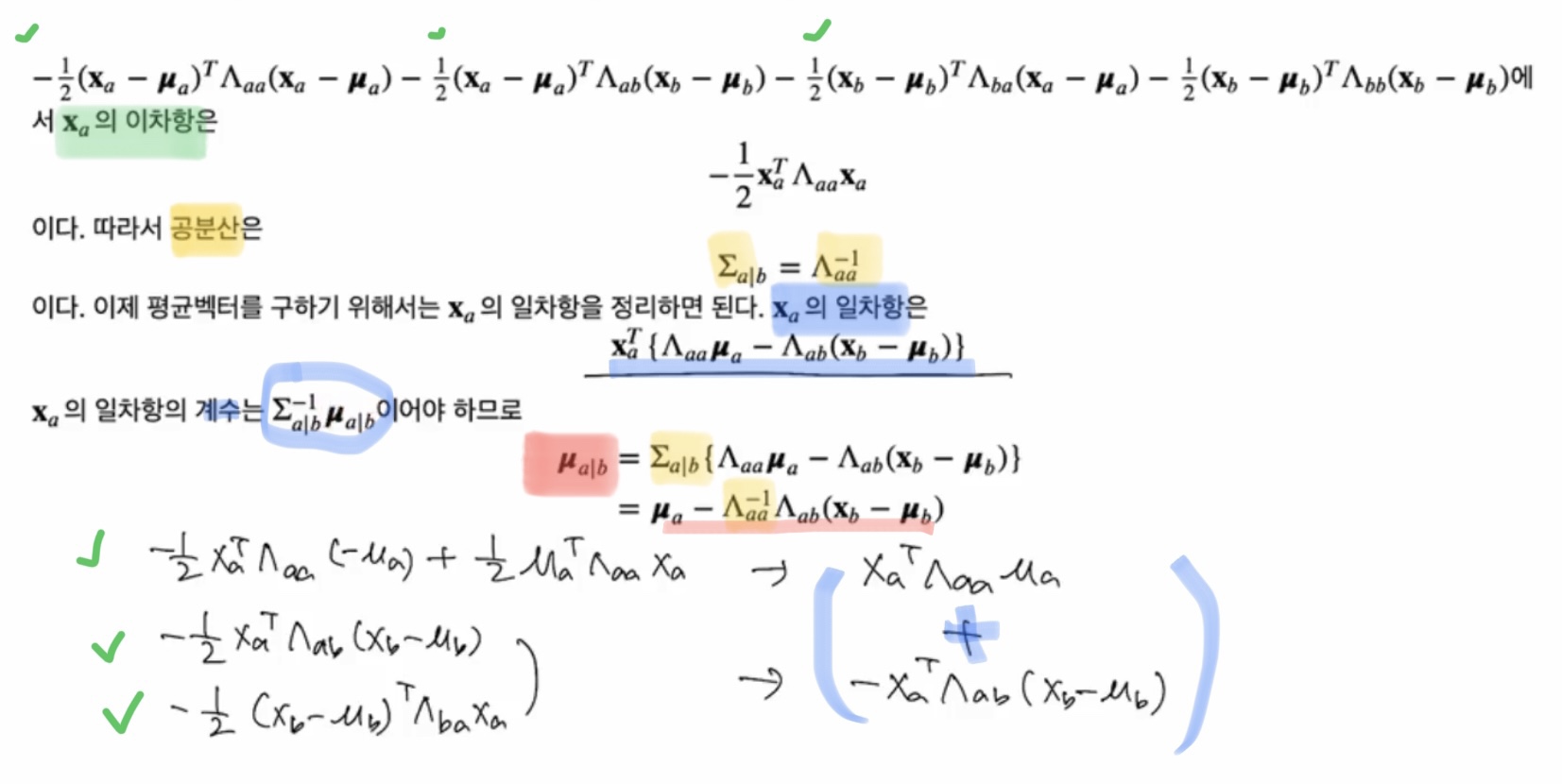
먼저, Xa의 이차항을 찾고
Xa의 일차항을 정리하면 된다
Xa의 일차항은 Xa의 transpose 와 계수의 곱
Xa의 “평균” 부분은 빨간색 부분
“공분산” 부분은 노란색 부분, 공분산은 Lambda aa의 역행렬
4. 주변 가우시안 분포(Marginal Gaussian Distributions)
overview

단계별로 나눠서 이해해보면

주변 가우시안 분포에서는 타우도 신경써줘야



결론적으로 X에 대한 확률변수 주어져있고 그것을 a와 b로 나눴을 때
Xa의 평균 벡터는 mu a, Xa의 공분산은 aa의 공분산
5. 가우시안 분포를 위한 베이즈 정리(Bayes’ Theorem for Gaussian Variables)

p(x) = x는 mu라는 평균 벡터를 가지고 있고, lambda를 precision(정확도)의 행렬로 가지고 있다
p(y|x) = y는 ax+b 라는 평균 벡터를 가지고 있고, ?? 를 precision(정확도)의 행렬로 가지고 있다
x와 y의 결합확률분포를 구하면 모든 주변확률과 조건부확률을 알 수 있다

'Math' 카테고리의 다른 글
| Machine Learning 기초 (2) - 선형 분류 Linear Models for Classification (0) | 2021.06.12 |
|---|---|
| Machine Learning 기초 (1) - 선형 회귀 Linear Models for Regression (0) | 2021.06.12 |
| 확률분포 (2) - 이산확률분포 다항변수 (0) | 2021.06.07 |
| 확률분포 (1) - 이산확률분포 이항변수 (0) | 2021.06.07 |
| 결정이론 (3) - 결정 문제를 위한 방법들 (2) | 2021.06.05 |